単純ベイズ分類器(naive bayes)

本章では観測データ x について、それが所属されるクラスの間に確率分布が仮定される分類問題を、 単純ベイズ分類器(naive bayes) を中心に説明する。

導入; 前提知識

単純ベイズ分類器を扱うために前提知識について触れておく。

条件付き確率

事象Aが起きた前提で事象Bが起きる確率を条件付き確率といい、以下の式で定義される。

$P(B | A) = \frac{P(A \cap B)}{P(A)}$

特に、

$P(B | A) = \frac{P(A \cap B)}{P(A)} \\ P(A)P(B | A) = P(A \cap B)$

ベイズの定理

事象 $A, B$ について、 $P(A | B), P(A), P(B)$がわかっているとき、 $P(B | A)$を以下の式で求めることができる。

$P(B | A) = \frac{P(B)P(A | B)}{P(A)}$

これをベイズの定理とよぶ。導出は以下。

$P(B | A) = \frac{P(B \cap A)}{P(A)} \\ ここで、 \\ P(B \cap A) = P(B)P(A | B) \\ から、 \\ P(B | A) = \frac{P(B)P(A | B)}{P(A)}$

尤度

データ $\mathbf{x}$ がクラス $C$ に属する尤もらしさとは、データ $\mathbf{x}$ となるもののうちクラス $C$ に属する割合 $p(C | \mathbf{x})$であり、これを尤度という。

統計学でのベイズの定理

求める$P(B|A)$を、$A$が起きた後の 事後確率 と呼ぶ。 $P(B)$は$A$を考えない時の生起確率であり、事後確率に対して 事前確率 と呼ぶ。 $P(A)$は独立な$B_i$に対して$P(A)=\sum P(B_i \cap A)$であることから、$P(B|A)$についての 周辺確率 と呼ぶ。

これらを用いてベイズの定理を考えると、以下のように解釈できる。

$P(B | A) = \frac{P(B)P(A | B)}{P(A)} \\ P(B | A) = \frac{P(A | B)}{P(A)} \times P(B) \\ 事後確率 = \frac{尤度}{周辺確率} \times 事前確率$

単純ベイズ分類器

ある特徴ベクトルがどのクラスに分類されるかを決定する写像を 分類器 とよぶ。ここでは先ほどのベイズの定理を用いた 単純ベイズ分類器(naive bayes) を紹介する。

「特徴ベクトル $\mathbf{x_j}$ がクラス $C_i (i=1,2,\cdots,n)$に分類される」という学習によって $p(x|C_i), p(\mathbf{x}), p(C_i)$を知っている時、ある $\mathbf{x}$ がクラス $C_i$ に属する尤度 $p(C_i|\mathbf{x})$ はベイズの定理から、

$P(C_i | \mathbf{x}) = \frac{p(\mathbf{x} | C_i)}{p(\mathbf{x})} \times P(C_i)$

で導くことができる。ここで、$C_i$と$C_j$を比較したとき、$\mathbf{x}$ は尤度が高い方のクラスに属する方が尤もらしいといえる。すなわち、

$p(C_i | \mathbf{x}) = \frac{P(C_i)p(\mathbf{x} | C_i)}{p(\mathbf{x})} \left\{\begin{matrix} > \\ < \end{matrix}\right\} \frac{P(C_j)p(\mathbf{x} | C_j)}{p(\mathbf{x})}= p(C_j | \mathbf{x}) \left\{\begin{matrix} \Rightarrow C_i \\ \Rightarrow C_j \end{matrix}\right\}$

ここで $p(\mathbf{x})$ をはらって、

$P(C_i)p(\mathbf{x} | C_i) \left\{\begin{matrix} > \\ < \end{matrix}\right\} P(C_j)p(\mathbf{x} | C_j) \left\{\begin{matrix} \Rightarrow C_i \\ \Rightarrow C_j \end{matrix}\right\}$

を得る。全クラス$C_i (i=1,2,\cdots,n)$に対して行えばよいので、単純ベイズ分類器は以下の式で分類を行う。

$\max_{i} p(x | C_i)P(C_i)$

また、クラス$C_i$と$C_j$についての識別境界は

$P(C_i | \mathbf{x}) = \frac{p(\mathbf{x} | C_i)}{p(\mathbf{x})} \times P(C_i) = \frac{p(\mathbf{x} | C_j)}{p(\mathbf{x})} \times P(C_j) = P(C_j | \mathbf{x})$

にある。以下の図で言うと真の分布に対して識別境界$\theta$が設けられ、左側に行くと$C_i$の方が事後確率が高いため$C_i$に、右側に行くと$C_j$の方が事後確率が高いため$C_j$に識別される。

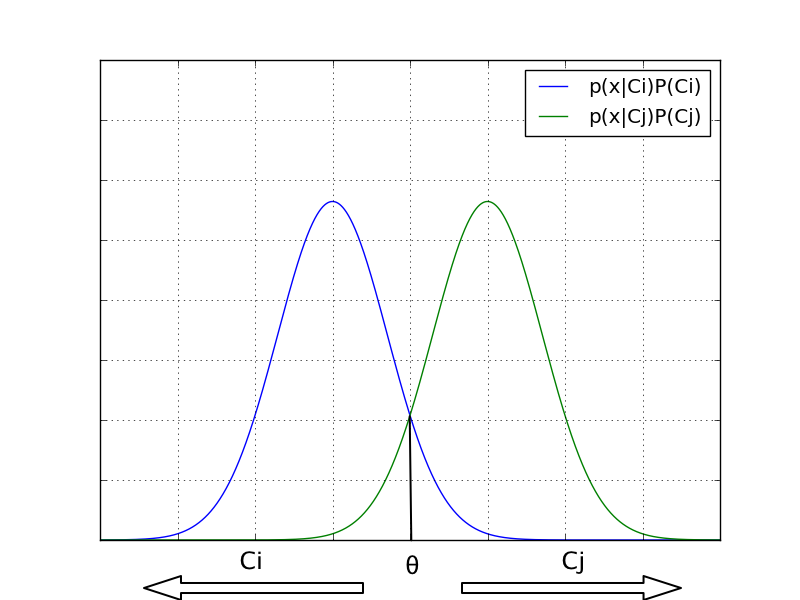
誤り率

あるクラス$C_i$と$C_j$に同様の特徴が現れた時、分類器は分類を誤る場合がある。誤りが発生する確率を 誤り率$\varepsilon$ とする。単純ベイズ分類器はクラス$C_i$の事後確率がクラス$C_j$の事後確率より大きい時にクラス$C_i$に分類するため、誤りは事後確率が小さい方が正しい分類である確率すなわち

$\varepsilon(\mathbf{x}) = \min [P(C_i|\mathbf{x}), P(C_j|\mathbf{x})]$

となる。

ベイズ誤り率

ベイズ誤り率は誤り率の期待値として表される。 $C_i$に認識される領域を$R_i$、 $C_j$に認識される領域を$R_j$として、期待値は

$\begin{align} &\int_{R_i+R_j} \varepsilon(\mathbf{x})p(\mathbf{x}) dx \\ &= \int_{R_i+R_j} \min [P(C_i|\mathbf{x}), P(C_j|\mathbf{x})]p{x} dx \\ &= \int_{R_i+R_j} \min [\frac{p(\mathbf{x}|C_i)P(C_i)}{p(\mathbf{x})}, \frac{p(\mathbf{x}|C_j)P(C_j)}{p(\mathbf{x})}]p{x} dx \\ &= \int_{R_i+R_j} \min [p(\mathbf{x}|C_i)P(C_i), p(\mathbf{x}|C_j)P(C_j)] dx \end{align}$

$\min [p(\mathbf{x}|C_i)P(C_i), p(\mathbf{x}|C_j)P(C_j)]$は、領域$R_j$のうち$C_i$であるものと領域$R_i$のうち$C_j$であるものの和（以下の図）であるため、

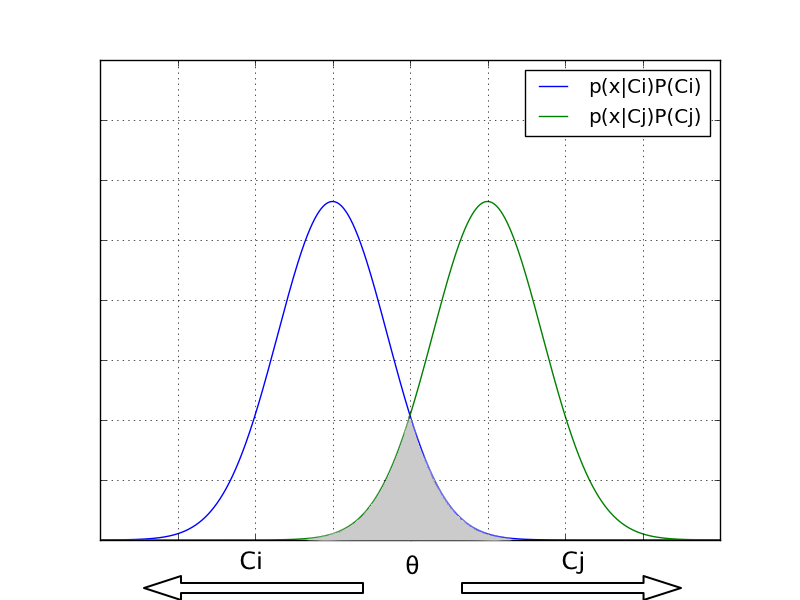
$\begin{align} &\int_{R_i+R_j} \min [p(\mathbf{x}|C_i)P(C_i), p(\mathbf{x}|C_j)P(C_j)] dx \\ &= \int_{R_i+R_j} P(C_i, \mathbf{x} \in R_j) + P(C_j, \mathbf{x} \in R_i) dx \\ &= \int_{R_j} P(\mathbf{x}|C_i)P(C_i) dx + \int_{R_i} P(\mathbf{x}|C_j)P(C_j) dx \\ \end{align}$

として表現できる。

ベイズの識別境界は誤り率最小

ここで、ベイズの識別境界とは別の識別境界をしいてみる。例えば以下の$\theta^*$を考えた時、ベイズ誤り率は灰色に塗られた部分の面積となる。

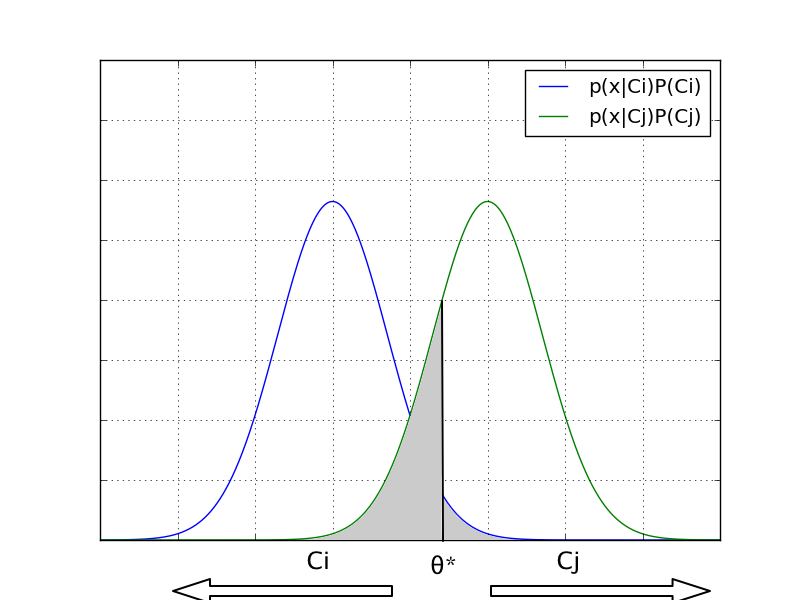
これはベイズの識別境界と比べて、薄い灰色の分だけ誤り率が多く、これを小さくしていくと最終的にベイズの識別境界に収束することがわかる。

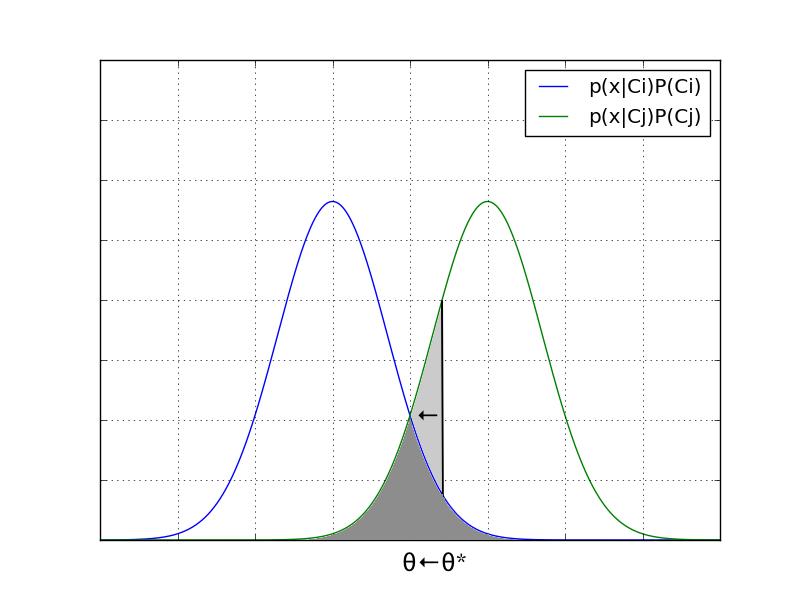
損失

健康な人(1)と病気の人(2)を判断する時の誤認識には、健康な人を病気であると認識する$\varepsilon_{12}$と病気の人を健康であると認識する$\varepsilon_{21}$が存在する。ここで単純ベイズ分類器は誤り最小となる境界を設けるが、明らかに 病気の人を健康であると誤診 する方が危険であるため、どうにかしてこの誤診を減らしたい。ここでは損失の導入で $\varepsilon_{21}$の期待値を減らすことができることを示す。

最小損失基準

真のクラスが$C_i$であるデータを$C_j$と誤ったときの危険性を損失$Lij$で表す。 K個のクラスがあるとき$Lij$を要素とする$K \times K$の行列が作られる。これを 損失行列 という。

ここから、データ$\mathbf{x}$をクラス$C_i$と判断した時に発生する損失は、

$r(C_i | \mathbf{x}) = \sum_{k=1}^K L_{ik}P(C_k | \mathbf{x})$

となる。この関数を使って、識別規則を「損失が最も小さいクラスに識別すること」 とする。すなわち

$識別クラス = \min_{i} r(C_i | \mathbf{x})$

これを最小損失基準という。